The RGB color Space
TV screens and computer displays, whether old-style cathode ray tube (CRT) or current technology liquid crystal display (LCD) use the same principle to display colors as the eye uses to receive color, namely by building up the color with differing amounts of just three components: blue, green and red. Examine your TV or computer screen with a magnifying glass and you will see that each spot of color is, indeed, a small cluster of three colored spots. The CRT displays of older TV's and computers generated these spots by focusing separate electron beams on each of three types of phosphor compounds which respond by glowing in the different colors. The modern LCD screens electronically open and close minute "shutters" (the liquid crystals) that allow varying amounts of white light to pass from behind and through red, green or blue filters. There are, of course, thousands of these clusters on the screen: a modern HD LCD computer display has a "screen resolution" of 1920 x 1080 pixels, requires 2,073,600 - yes over two million separate clusters of these three liquid crystal light filters. And each one of those 12 million crystals is individually driven to generate your display.
| This animation shows a shows a 5x5x5 matrix of 125 uniquely colored balls which are colored according to the RGB color space. At the lowest apex we have White - the combination of full intensity of the three colors, and at the top, Black, which is the absence of any color. At the three apexes immediately below the Black we have the pure Red Green and Blue colored balls. At the three apexes immediately above the White, we have the three compound colors, Yellow, Cyan and Magenta. |  |
A cube has six faces, 8 corners or vertices and 12 edges. I have chosen to display this cube rotating around an axis on the diagonal between the black and the white vertices. Three of the remaining six vertices are colored red, blue and green known as RGB. The three remaining vertices are colored with the intermediate colors of cyan, half way between blue and green, yellow, between red and green and magenta between red and blue. Each remaining color contains amounts of red, green and blue depending on their respective distance from the the primary RGB points; with increasing amounts towards the white point, which contains the maximum quantities of red, blue and green, and decreasing quantities towards the black point which contains no amount of color.
Of course, this is all done mathematically by assigning the amount of RGB in each of the colors, with 256 values ranging from 0 to 255, so red is 255(R),0(G),0(B), white is 255,255,255, black 0,0,0, and cyan 0,255, 255. I have displayed only 125 colors out of the possible 16 million (256x256x256 = 16,777,216) colors that can be displayed on a computer monitor.
The colors inside the cube are colored on the same principle of their distance from the RGB in either the white or black direction determining the amount of the RGB primary colors. The inside of the cube contains the murky shades of brown, khaki and purple and the pastel shades of turquoise, lemon and mauve.
Just for fun, I have generated the four cross-sections of the cube at the centre through a diagonal axis from each of the four pairs of apexes: Black-White, Red-Cyan, Green-Magenta and Blue-Yellow. Surprisingly perhaps to many, these cross-sections are hexagonal as you can see from this animation of the plane perpendicular to the Blue-Yellow axis:
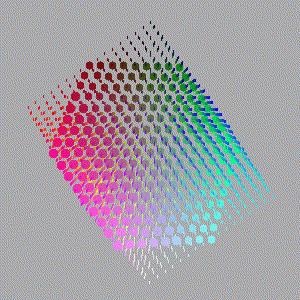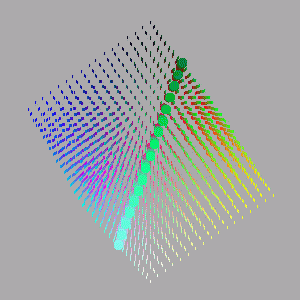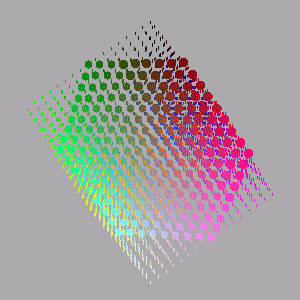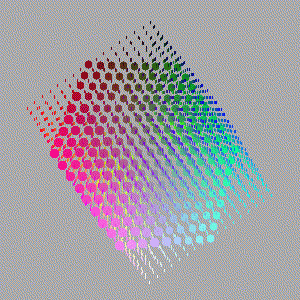
The images below are animations of slices through the cube along an axis between a pair of diagonally opposite apexes. The image starts as a point then grows as a triangle. The triangle then morphs into a hexagon at the centre of the cube and then retreats back to a triangle which disappears to a dot.
 The Black-White axis. |
 The Red-Cyan axis |
 The Green-Magenta axis |
 The Blue-Yellow axis (as in the animation above) |